του Παντελή Σαββίδη
Σε μια εποχή πνευματικής πενίας, η είδηση ότι ο νεαρός Επίκουρος Καθηγητής του Μαθηματικού Τμήματος του ΑΠΘ Δημήτριος Νταλαμπέκος επελέγη —ο μόνος από όλα τα ελληνικά ΑΕΙ— για χρηματοδότηση με 1,3 εκατ. ευρώ/5ετία από το ιδιαίτερα ανταγωνιστικό πρόγραμμα ERC Starting Grants 2025 προκάλεσε αληθινή ανακούφιση. Καθώς η κρίση βαθαίνει, η κοινωνία αναζητά σημεία αναφοράς· και η επιτυχία του κ. Νταλαμπέκου λειτούργησε συμβολικά: μπορούμε, έχουμε ανθρώπους και ιδέες — αυτό που συχνά λείπει είναι η βούληση και η οργάνωση του κράτους. Το αντικείμενο του νέου έργου; Τα fractals — «τα πιο πολύπλοκα σχήματα της φύσης», όπως σημειώνει ο ίδιος.
Η γεωμετρία, για αιώνες, υπήρξε η τέχνη της τάξης και της καθαρότητας. Από τα αξιώματα του Ευκλείδη μέχρι την επανάσταση της μη ευκλείδειας γεωμετρίας τον 19ο αιώνα, πιστέψαμε ότι ο κόσμος χωρά σε ευθείες, κύκλους και κανονικά πολύγωνα. Η φύση όμως αντιστέκεται: ακτογραμμές, σύννεφα, ορεινοί όγκοι, αγγειακά δίκτυα — τίποτε από αυτά δεν μοιάζει με τα «καθαρά» σχήματα των σχολικών εγχειριδίων.
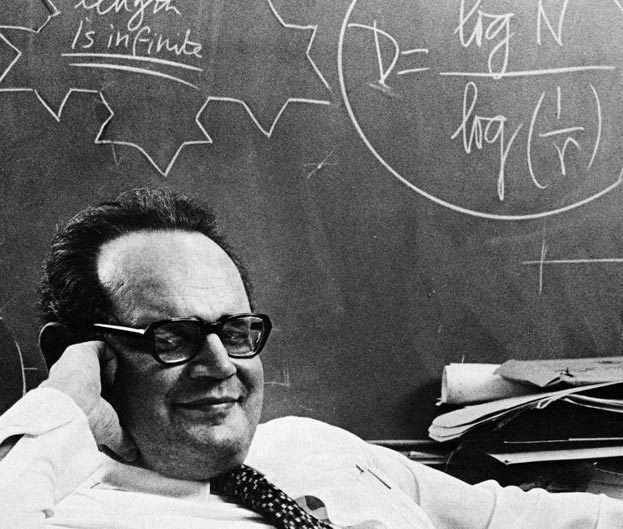
Η απάντηση ήρθε από μια τρίτη γεωμετρία, μετά την ευκλείδεια και τη μη ευκλείδεια: τη γεωμετρία των fractals. Ο «πατέρας» της, ο Μπενουά Μάντελμπροτ, δεν προσπάθησε να εξημερώσει τη φύση — αντίθετα, έφτιαξε μια γεωμετρία που προσαρμόζεται στην ίδια την αταξία της. Η ιστορία των fractals, βέβαια, ξεκινά πριν τον Μάντελμπροτ: ο Καντόρ, ο Πουανκαρέ, ο Πέανo και άλλα «ανήσυχα πνεύματα» του τέλους του 19ου αιώνα εισήγαγαν τα περίφημα «μαθηματικά τέρατα» — καμπύλες και σύνολα που έμοιαζαν να προκαλούν τη διαίσθηση. Η καμπύλη του Πέανo που «στρώνει» ολόκληρο ένα επίπεδο, η καμπύλη του Κοch με άπειρο μήκος και πεπερασμένη επιφάνεια: ανωμαλίες που δεν χωρούσαν στον κλασικό κανόνα.
Κάποια στιγμή τα «τέρατα» αυτά έπρεπε να αποκτήσουν όνομα. Ο Μάντελμπροτ τούς έδωσε ταυτότητα: fractal, από το λατινικό fractus («σπασμένος», «θρυμματισμένος»). Το όνομα υπονοεί τόσο τον τεμαχισμό όσο και την κλασματική διάσταση, τη «μεταξύ» διάσταση που δεν είναι ούτε 1 ούτε 2 αλλά κάτι ενδιάμεσο. « “Το να ονομάζεις σημαίνει να γνωρίζεις”», έγραψε στο The Fractal Geometry of Nature (1982). Με την ονοματοδοσία, η «γκαλερί των τεράτων» απέκτησε τάξη — και η γεωμετρία άνοιξε ένα νέο κεφάλαιο.

Η τρίτη γεωμετρία, με μια ιδιότητα-κλειδί
Αν η ευκλείδεια γεωμετρία περιγράφει τον «καθημερινό» χώρο και η μη ευκλείδεια τους καμπυλωμένους χώρους της σχετικότητας, η γεωμετρία των fractals εξηγεί τα ακανόνιστα σχήματα που γεμίζουν τον φυσικό κόσμο. Κύριο γνώρισμά τους η “αυτοομοιότητα”: ό,τι και αν μεγεθύνεις, βλέπεις μοτίβα που θυμίζουν το όλον. Στην ακτογραμμή, σε κλίμακα χώρας ή κόλπου, επανεμφανίζεται η ίδια «οδοντωτή» υπογραφή. Αυτός ο «νόμος της επανάληψης» τα ξεχωρίζει από οτιδήποτε γνώριζε η κλασική γεωμετρία.
Fractals και μη γραμμικά συστήματα
Η άνθηση των fractals δεν ήταν τυχαία· συνέπεσε με την άνοδο της θεωρίας των μη γραμμικών συστημάτων και της χαοτικής δυναμικής. Στα γραμμικά μοντέλα οι μικρές αλλαγές δίνουν μικρές διαφορές. Στα μη γραμμικά, μικροσκοπικές μεταβολές εκρήγνυνται σε πολυπλοκότητα — το «φαινόμενο της πεταλούδας». Εκεί, τα fractals εμφανίζονται ως αποτυπώματα του χάους.

Η εκρηκτική εξέλιξη των ηλεκτρονικών υπολογιστών επέτρεψε για πρώτη φορά να δούμε αυτά τα αποτυπώματα. Το “σύνολο Mandelbrot” —που ξεπηδά από την απλούστατη επανάληψη ενός κανόνα— αποκάλυψε ένα άπειρο σύμπαν μορφών. Η εικόνα του έγινε σύμβολο: μαθηματικό αντικείμενο, ψηφιακή τέχνη, έμπνευση για σχεδιαστές και μουσικούς.
Ένα κοινωνικό φαινόμενο
Τα fractals ξεπέρασαν την ακαδημαϊκή σφαίρα. Γεννήθηκαν κοινότητες, λέσχες, πρότζεκτ τέχνης. Οι «σιωπηλοί» μαθηματικοί βρέθηκαν στο επίκεντρο της δημοσιότητας. Δεν είναι τυχαίο ότι ο John Archibald Wheeler, πρωτοπόρος της κβαντικής θεωρίας, προφήτευσε: «Στο μέλλον, κανείς δεν θα θεωρείται ότι μετέχει της επιστημονικής παιδείας, αν δεν είναι αρκετά εξοικειωμένος με τα fractals». Η κατανόησή τους δεν είναι πολυτέλεια· είναι γλώσσα του σύγχρονου κόσμου.
Μέρος, όλον και «συναρτησιακότητα»
Η φιλοσοφική γέφυρα είναι εξίσου γόνιμη. Από τους προσωκρατικούς έως τον 20ό αιώνα, το ζεύγος «μέρος–όλον» βασανίζει τη σκέψη. Είναι το όλον άθροισμα μερών; Στα fractals, η απάντηση γέρνει αλλιώς: το όλον δεν είναι πρόσθεση· είναι αποτέλεσμα μιας συνάρτησης. Η συνάρτηση-γεννήτορας ενώνει και «περιχωρεί» τα μέρη. Έτσι, κάθε θραύσμα φέρει την υπογραφή του όλου — όχι ως αντίγραφο, αλλά ως έκφραση της ίδιας γενετικής διαδικασίας.
Ούτε ο απλός τεμαχισμός (“fragmentation”) ούτε ένας αφελής ολισμός (“holism”) αρκούν. Ο πραγματικός αντίποδας του τεμαχισμού είναι η “συναρτησιακότητα”: η έμφαση στη σχέση που γεννά και συγκρατεί το πολλαπλό. Tο όλον που εκλαμβάνεται σε αντιδιαστολή με το μερικό καταντά και αυτό μερικό». Μόνο όταν δούμε τον κανόνα που παράγει μαζί μέρη και όλον, ξεφεύγουμε από τη δυαδικότητα.
Δύο εμβληματικά παραδείγματα
Mandelbrot: μια απλή επανάληψη κανόνα γεννά άπειρη ποικιλία· κάθε μικρόκοσμος μοιάζει με το όλον.
Koch: άπειρο μήκος, πεπερασμένη επιφάνεια· κάθε τμήμα επαναφέρει το μοτίβο — το μερικό ενσωματώνει το ολικό.

Η επιτυχία του Μάντελμπροτ ήταν εργαλειακή: έδειξε πώς ο ίδιος κανόνας παράγει απέραντη πολυπλοκότητα χωρίς να ακυρώνει την ταυτότητα των μερών.
Η μαθηματική συνάρτηση γίνεται έτσι μοντέλο μιας βαθύτερης θέσης: ούτε «καθαρό όλον» ούτε «σκόρπια μέρη», αλλά σχέση που επανεμφανίζεται σε κάθε κλίμακα.
Τι ακριβώς θα κάνει ο Δημήτριος Νταλαμπέκος (ERC GRComPaS)
Πέρα από τον συμβολισμό, το έργο του κ. Νταλαμπέκου έχει σαφές επιστημονικό διακύβευμα και μια αποστολή που συνομιλεί άμεσα με όσα προαναφέραμε. Ο ίδιος το συνοψίζει με καθαρότητα: *«Εύχομαι αυτό το πρόγραμμα να δημιουργήσει ευκαιρίες για νέους και να τους δώσει θάρρος να κυνηγήσουν τα όνειρά τους — ιδανικά χωρίς να χρειαστεί να ξενιτευτούν».
Ακολουθούν οι βασικοί άξονες του προγράμματος GRComPaS:

1) Γιατί fractals — και γιατί τώρα
Τα fractals είναι το αντίθετο των λείων σχημάτων: δεν είναι ομαλά, έχουν γωνιώδη/πολύπλοκη υφή και συχνά επαναλαμβανόμενα μοτίβα. Εμφανίζονται παντού: ακτογραμμές, ορεινά ανάγλυφα, ποτάμια δίκτυα, αλλά και σε «καθαρά» θεωρητικές περιοχές: Μιγαδικά Δυναμικά Συστήματα, Γεωμετρική Θεωρία Ομάδων, Μετρική Γεωμετρία, Θεωρία Πιθανοτήτων. Η κλασική θεωρία για λεία σχήματα αναπτύχθηκε εντυπωσιακά από τον Γκάους και τους επιγόνους του· για τα fractals, η συστηματική κατανόηση είναι υπό διαμόρφωση μόλις τις τελευταίες δεκαετίες — η οπτικοποίηση μέσω υπολογιστών έπαιξε τεράστιο ρόλο.
2) Το «πρόβλημα του μετασχηματισμού»: από το τραχύ στο λείο
Ο κεντρικός στόχος του GRComPaS είναι φιλόδοξος και καίριος: μπορεί ένα fractal να μετασχηματιστεί (σαν εύπλαστο υλικό) σε λείο* σχήμα;
Αν ναι, θα μπορέσουμε να μεταφέρουμε ώριμα εργαλεία της λείας γεωμετρίας στη μελέτη μη λείων σχημάτων — να «δανειστούμε» ομαλότητα για να κατανοήσουμε την τραχύτητα.
Η αναλογία είναι καθημερινή και ισχυρή: η χαρτογράφηση. Για να «στρώσουμε» τη σφαίρα της Γης σε επίπεδο χάρτη, δεχόμαστε παραμορφώσεις. Το κρίσιμο είναι να διατηρούνται οι γωνίες (σύμμορφη απεικόνιση), ώστε οι κατευθύνσεις να αποτυπώνονται αξιόπιστα — γι’ αυτό οι χάρτες είναι χρήσιμοι στη ναυσιπλοΐα.
Το έργο επιχειρεί κάτι ανάλογο: μετασχηματισμούς που, όσο γίνεται, διατηρούν γωνίες (conformal) για να «ξεδιπλώσουν» ένα fractal σε λείο αντικείμενο, **χωρίς** να χαθεί η δομική του πληροφορία. Αν αυτό επιτευχθεί σε γενικότητα, θα αποτελέσει **θεμελιακή γέφυρα** ανάμεσα σε δύο μέχρι σήμερα «ασύμβατους» κόσμους.
3) Γιατί έχει σημασία (ακόμα κι αν οι εφαρμογές αργήσουν)
Το GRComPaS αγγίζει ανοικτά προβλήματα δεκαετιών σε πολλές περιοχές των καθαρών μαθηματικών· μια επιτυχής έκβαση θα έχει δομικές συνέπειες για τη θεωρία. Όσο για εφαρμογές εκτός μαθηματικών, κανείς δεν υπόσχεται «άμεσο θαύμα» — και σωστά. Η ιστορία διδάσκει ότι η θεμελιώδης θεωρία συχνά καρποφορεί αργότερα: η μαθηματική ανάλυση του Fourier γράφτηκε τον 19ο αιώνα και έγινε ραχοκοκαλιά των τηλεπικοινωνιών έναν αιώνα μετά.
4) Ένα «καθαρό» εργαστήριο για το χάος: τα μιγαδικά δυναμικά
Ο καιρός είναι χαοτικός, με αμέτρητες παραμέτρους — γι’ αυτό δεν προβλέπεται αξιόπιστα σε βάθος μηνών. Τα Μιγαδικά Δυναμικά Συστήματα είναι, θα λέγαμε, το «καθαρό εργαστήριο» του χάους: λιγότερες παράμετροι, περισσότερα εργαλεία. Κι όμως, ακόμα και τα απλούστερα μοντέλα (μια μόνο παράμετρος!) παραμένουν μερικώς αχαρτογράφητα. Το GRComPaS στοχεύει να φωτίσει ακριβώς αυτή τη ζώνη, προσφέροντας καλύτερη κατανόηση της γεωμετρίας που αναδύεται από την επανάληψη ενός κανόνα.
Τι «νέο» φέρνει αυτή η έρευνα στο ευρύτερο αφήγημα των fractals
- Από το όνομα στην πράξη
Ο Μάντελμπροτ μάς έδωσε τη λέξη και τη θέαση του κόσμου ως fractal. Η έρευνα τύπου GRComPaS επιχειρεί το επόμενο βήμα: λειτουργικές «γέφυρες» ανάμεσα στο τραχύ και το λείο. Δηλαδή, όχι μόνο να ονoμάσουμε και να δείξουμε την αυτοομοιότητα, αλλά να μεταφέρουμε όλη τη βαριά εργαλειοθήκη της λείας γεωμετρίας στον «άγριο» χώρο των fractals.
- Η φιλοσοφική έννοια της «συναρτησιακότητας» σε τεχνική εκδοχή
Όταν λέμε «το όλον είναι συνάρτηση», εδώ έχουμε κυριολεξία: επιδιώκουμε συγκεκριμένους μετασχηματισμούς που αποκαλύπτουν τη συγγένεια (και τη μεταφερσιμότητα εργαλείων) μεταξύ κόσμων που φαίνονται ασύμβατοι. Αυτό «προσγειώνει» την ιδέα μέρους–όλου σε υπολογίσιμα σχήματα.
- Μια νέα κοινή γλώσσα
Η συνάντηση πληροφορικής και δυναμικών συστημάτων ώθησε την έρευνα των fractals. Η προσπάθεια για «σύμμορφους όσο γίνεται» μετασχηματισμούς δημιουργεί μια νέα κοινή γλώσσα ανάμεσα σε καθαρά μαθηματικά, οπτικοποίηση, ακόμη και γεωεπιστήμες (αναγλύφου/χαρτογράφησης). Το πώς θα παραμορφώσεις για να μην χάσεις το ουσιώδες είναι το νέο «χρυσό ερώτημα».
Επιστροφή στο αρχικό ερώτημα: είναι τα fractals «η τρίτη γεωμετρία»;
Με όρους ιστορίας των ιδεών, ναι: τα fractals συγκροτούν ένα τρίτο γεωμετρικό παράδειγμα που συμπληρώνει τα δύο κλασικά. Δεν αντικαθιστούν την ευκλείδεια ή τη μη ευκλείδεια γεωμετρία· προσφέρουν το πλαίσιο για να περιγράψουμε τραχιές μορφές και πολυκλιμακικές δομές. Είναι η γεωμετρία του «ανάμεσα»: ούτε εντελώς λεία ούτε άναρχα χαώδη, αλλά αυτοομοιόμορφα οργανωμένη.
Επιστήμη με ορίζοντα και κοινωνικό νόημα
Τα fractals μας διδάσκουν ότι ο κόσμος δεν είναι ούτε ψυχρή κανονικότητα ούτε τυφλή αταξία. Είναι μια αέναη επανάληψη απλών κανόνων που γεννούν ανεξάντλητη πολυπλοκότητα. Γι’ αυτό η γοητεία τους ξεπερνά τα όρια της μαθηματικής αίθουσας: γίνονται γέφυρα με τη φιλοσοφία, την τέχνη, ακόμη και την καθημερινή μας διαίσθηση για το «πώς χτίζεται» το πραγματικό.
Η επιτυχία του Δημήτρη Νταλαμπέκου δεν είναι μόνο προσωπικό επιστημονικό επίτευγμα. Είναι υπόσχεση για δομική πρόοδο σε προβλήματα που στέκουν ανοιχτά δεκαετίες· είναι και σύμβολο ότι αυτή η χώρα μπορεί να παράγει έρευνα πρώτης γραμμής. Όπως ευχήθηκε ο ίδιος, ας γίνει αφορμή να παραμείνουν περισσότεροι νέοι εδώ, να τολμήσουν υψηλή επιστήμη χωρίς να ξενιτευτούν. Και ας μάθουμε όλοι να «διαβάζουμε» τα fractals — όχι μόνο σαν ωραίες εικόνες, αλλά σαν γλώσσα που αποκαλύπτει πώς το μέρος και το όλον συνδέονται από μια συνάρτηση που επαναλαμβάνεται, υπομονετικά, στο άπειρο.
*Μέρος αυτού του κειμένου δημοσιεύθηκε στην εφημερίδα “Θεσσαλονίκη” Σάββατο 27.09.25
THE_2709_045_CMYK




«Όπως ευχήθηκε ο ίδιος, ας γίνει αφορμή να παραμείνουν περισσότεροι νέοι εδώ, να τολμήσουν υψηλή επιστήμη χωρίς να ξενιτευτούν.»
Σπουδαῖα ἐπιτεύγματα ἀπὸ ἄξιο ἄνθρωπο καὶ εὖγε. Μακάρι νὰ γίνει ἀφορμή. Ὑπάρχουν πολλοὶ ἄξιοι Ἕλληνες. Ἀλλὰ χρειάζεται καὶ κάτι ποὺ λείπει καιρό, ἡ ἀξιοκρατία ὡς θεμέλιος λίθος εὐημερούσας κοινωνίας. Καὶ αὐτὸ πρέπει νὰ τὸ προσπαθήσουμε συνειδητὰ ἂν θέλουμε νὰ ὑπάρχουμε. Νὰ δοῦμε καὶ νὰ βροῦμε πῶς θὰ ἐπιστρέψει ἡ ἀξιοκρατία στὴν χώρα. Ἐδῶ ποὺ ἔχει ἀνθίσει στὸ παρελθόν. Ὑπάρχει πεδίο ἔρευνας ἀκόμα καὶ γιὰ τὸ παρελθόν. Μία πρόσφατη ἀνάρτηση γιὰ τὴν Θόλο τῆς Ἐπιδαύρου,
https://www.epidavrosnews.com/2019/10/06/tholosepidayros/
δείχνει τὶς ἀστρονομικὲς ἀποτυπώσεις στὸ Ἀσκληπιεῖο. Τὰ Ἀσκληπιεία μόλις τώρα ἀρχίζουν νὰ ἐρευνῶνται.
“Νὰ δοῦμε καὶ νὰ βροῦμε πῶς θὰ ἐπιστρέψει ἡ ἀξιοκρατία στὴν χώρα”
Για να επιστρέψει κάτι, πρέπει να υπήρχε. Υπήρχε ποτέ αξιοκρατία στο νεοελληνικό κράτος; Πήγαινε ποτέ κανείς μπροστά, αν δεν είχε μπάρμπα στην Κορώνη; Πάντα το σόγια δεν έκαναν κουμάντο;
Ωραίος ο σύνδεσμος που έβαλες, Ελένη.
Καλὰ τὸ θέτεις στὸ νεοελληνικὸ κράτος. Εἶναι θέμα ἀξιῶν ὅμως. Ἡ ἐλὶτ τοῦ πνεύματος τῆς γενιᾶς τοῦ ‘30 δὲν κυνήγησε νὰ πάρει θέσεις ἂν καὶ θὰ μποροῦσαν, καὶ πολέμησαν γιὰ τὴν χώρα αὐτὴ καὶ προσέφεραν μὲ τὸ ταλέντο τους στὸν πολιτισμό μας, ἀλλὰ ὅπως ὁ Μίκης Θεοδωράκης καὶ στὴν διαπαιδαγώγηση τοῦ λαοῦ ὅπως γινόταν καὶ στὴν ἀρχαιότητα. Οὔτε εἶχαν ξενομανία, εἶχαν δέ ἐπικοινωνία μὲ τὴν Εὐρωπαϊκὴ διανόηση.
Τί παιδεία εἶχαν αὐτοί;
Οἱ ἄνθρωποι ὅταν βοηθοῦνται νὰ ἀναπτύξουν τὶς ἱκανότητές τους εἶναι ἀξιοκρατία καὶ ἔχει ὄφελος ἡ κοινωνία. Ἡ παιδεία μας αὐτὸ θὰ ἔπρεπε νὰ ἔχει στόχο, ὅπως ἐφαρμόζουν στὶς βόρειες Σκανδιναβικὲς χῶρες. Ἐπίσης ἐκεῖ ἐκπαιδεύονται στὴν συλλογικὴ ἐργασία. Δὲν εἶναι αὐτονόητα αὐτά. Ἡ ὀργάνωση τῆς παιδείας ὥστε νὰ ταιριάζει στὸν Ἑλληνικὸ λαὸ καὶ ὄχι ἀπομίμηση τῶν ξένων προτύπων πρέπει νὰ εἶναι ἡ ἀπαρχὴ μιᾶς ἀναγέννησης. Ἀλλὰ πρέπει νὰ ξαναμπεῖ ὁ Ἑλληνικὸς πολιτισμὸς στὶς πραγματικές του διαστάσεις καὶ νὰ σταματήσουμε τὴν ξενομανία κατὰ τὸ κοινῶς λεγόμενο. Ἔχουμε μία διαφορὰ 400 ἐτῶν ὑποδούλωσης ἀλλὰ ἔχουμε καὶ ἕνα μπόνους, τὸν διαχρονικὸ Ἑλληνικὸ πολιτισμὸ στὸ πρωτότυπο. Καὶ οἱ Κινέζοι πῆραν τὴν δυτικὴ τεχνολογία ἀλλὰ τὴν στήριξαν στὴν δική τους ἐκπαίδευση καὶ στὸ δικό τους δυναμικὸ ποὺ ἔχει φτιάξει πρωτότυπο πολιτισμό. Ἡ προσωπικὴ ἐργασία καὶ ὄχι τὰ ἐπιδόματα φέρνουν ἀποτελέσματα.
Οι κάποιες εξαιρέσεις επιβεβαιώνουν τον κανόνα. Το νεοελληνικό κράτος δεν έχει κουλτούρα, παράδοση αξιοκρατίας, όπως οι σκανδιναβικές χώρες, οι ΗΠΑ και πολλά άλλα κράτη. Αυτό το δείξαμε αμέσως από την αρχή, όταν, σαν χθες, το 1827 φροντίσαμε να δολοφονήσομε τον πρώτο και πραγματικά καθ’ όλα άξιο κυβερνήτη μας. Γι’ αυτό σήμερα είμαστε στα χάλια που είμαστε, ασχέτως γενιάς τού ’30, δηλαδή κάποιων ανθρώπων.
Μην συγκρίνεις την μεταοθωμανική Ελλάδα με την Αρχαία, διότι φαίνεται ότι τίποτε δεν μάς έμεινε απ’ αυτήν, παρά μόνο τα ελαττώματά της (αδυμανία συνεργασίας, διχόνοια κλπ).
Οὔτε κουλτούρα, οὔτε παράδοση ἀξιοκρατίας, οὔτε παρελθόν. Κάθισαν, σκέφτηκαν, ἔφτιαξαν πλαίσιο ποὺ τοὺς ταιριάζει. Μὲ στόχους, μὲ feed back, μὲ συνέχεια. Σύγκρινε μὲ τὸ τί γίνεται στὴν δική μας παιδεία, στὴν χώρα μὲ τὴν τεράστια παράδοση πολιτισμοῦ. Ἡ ἀποδόμηση τί ἔκανε; Ἀντὶ νὰ ἐκτιμήσουν καί νά μελετήσουν τὰ καλά μας ποὺ δόθηκαν καὶ ἀλλοῦ, ὅπως εἶχε γίνει μὲ τὸν ἀρχαῖο μας πολιτισμό, ἀπαξίωσαν ὅλο αὐτὸ ποὺ εἶναι παραπάνω καὶ δὲν μποροῦν νὰ τὸ κατανοήσουν. Μένει τό `ξέρεις ποιός εἶμαι ἐγώ `; Σκέψου ἂν ὁ Θεὸς κάνει προσκλητήριο πόσοι θὰ ἐμφανισθοῦν σὰν Μεγαλέξανδροι.
“Κάθισαν, σκέφτηκαν, ἔφτιαξαν πλαίσιο ποὺ τοὺς ταιριάζει”
Ακριβώς, επειδή οι ίδιοι ήσαν ανάξιοι, δεν μπορούσαν να ενδιαφέρονται για την αξιοκρατία. Άλλως θα έβγαιναν ζημιωμέμοι.
“Σκέψου ἂν ὁ Θεὸς κάνει προσκλητήριο πόσοι θὰ ἐμφανισθοῦν σὰν Μεγαλέξανδροι.”
Ο Σκαρίμπας δεν είναι που έγραψε ότι ο Έλληνας, όταν κοιτάζει το εαυτό του στον καθρέπτη, βλέπει το Μέγα Αλέξανδρο και ποτέ τον Καραγκιόζη;